DPO 6th edition: Chapter 3.1-3.6
Link to corrected version of DPO section 3.5.5, on thermal expansion and haline contraction coefficients.
Supplemental:
DPO 6th edition Java Ocean Atlas examples text for DPO Chapter 3
pdf of powerpoint of Lecture II (density, potential density, neutral density, Brunt Vaisala frequency, sound speed, tracers)
Units. Officially we should be using mks units for everything. In reality, we often use cgs since our velocities are on the order of cm/sec rather than m/sec. We usually refer to depths in meters, and distances in kilometers. Most publications use decibars for pressure rather than Pascals. We usually use degrees Celsius rather than Kelvin, but care should be taken when doing heat calculations. Salinity officially has no units (see discussion below). In general be careful about units when doing calculations.
Units. The units
of force are (mass length / time^2) which you can remember
from Newton's Law F = ma. The units of pressure
are (force / length^2) or (mass /[length time^2]).
In the ocean, the downward force of gravity is balanced mostly by an upward pressure gradient force. That is, the water is not accelerating downwards - instead it is kept from collapsing by the upward pressure gradient. Therefore pressure increases with increasing depth.
The pressure at a given depth depends on the mass of water lying above that depth. (Hydrostatic equation given in class.) If the pressure change is 100 decibars (100 dbar), gravity g = 9.8 m/sec^2, and density is 1025 kg/m^3, then the depth change is 99.55 meter.
The total vertical variation in pressure in the ocean is thus from near zero (surface) to 10,000 dbar (deepest).
Horizontal pressure gradients drive the horizontal flows in the ocean (which are much much stronger than the vertical flows). The horizontal variation in pressure in the ocean is due entirely to variations in the mass distribution. Where the water column above a given depth (or rather geopotential surface, parallel to the geoid) is heavier because it is either heavier or thicker or both, the pressure will be greater. Note that the horizontal pressure differences which drive the ocean currents are on the order of a decibar over hundreds or thousands of kilometers, that is, much smaller than the change in pressure with depth.
How is pressure measured?
(1) Until recently, and possibly still in some laboratories, pressure was measured using a pair of reversing thermometers - one protected from seawater pressure by a vacuum and the other open to the seawater pressure. They were sent in a pair down to whatever depth, then flipped over, which cuts off the mercury in an ingenious small glass loop in the thermometer. They were brought back aboard and the difference between the mercury column length in the protected and unprotected thermometers was used to calculate the pressure.
(2) Quartz transducer now used with electronic instruments. The accuracy is 3 dbar and the precision is 0.5 dbar.
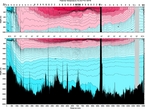
Figure. Depth versus pressure calculated from a CTD profile near Japan.
3.1. Temperature
Definition. Temperature is a thermodynamic property
of a fluid, and is due to
the activity of molecules and atoms in the fluid. The more the
activity (energy), the higher the temperature. Temperature is
a measure of the heat content. Heat and temperature are related
through the specific heat: (equation in class).
When the heat content is zero (no
activity), the temperature is absolute zero (on the Kelvin scale).
Units. Temperature units used in oceanography are degrees Celsius. For heat content and heat transport calculations, the Kelvin scale for temperature should be used. In the special case when mass transport is zero across the area chosen for the heat transport calculation, degrees Celsius can of course be used. Most oceanographic applications of heat transport rely on making such a mass balance. (See discussion in topic 3.) 0 C = 273.16 K. A change of 1 deg C is the same as a change of 1 deg K.
How is temperature measured? (1) Reversing mercury thermometers (see pressure discussion above). These were invented by Negretti and Zamba in 1874. Accuracy is 0.004C and precision is 0.002C. (2) Thermistors for electronic instruments, including replacement for reversing thermometer pairs. Quality varies significantly. The best thermistors commonly used in oceanographic instruments have and accuracy of 0.002C and precision of 0.0005-0.001C.
3.2. Heat
Heat per unit volume is computed from temperature
using Q = density*specific heat*T
where Q is heat/volume and T is temperature in degrees Kelvin.
(When making a heat calculation within the ocean, where pressure
is non-zero, use potential temperature, as defined below.)
mks units of heat are joules (i.e. an energy unit).
Heat change is expressed in Watts (i.e. joules/sec).
Heat flux is in Watts/meter^2 (energy per second per unit area).
To change the temperature by 1C in a column of water which is 100 m thick and 1 m^2 on the top and bottom, over a period of 30 days, requires what heat flux? The density of seawater is about 1025 kg/m^3 and the specific heat is about 3850 J/(kg C). The heat flux into the volume must then be density*specific heat*(delta T)*volume/(delta t) where T is temperature and t is time. This gives a heat change of 152 W. The heat flux through the surface area of 1m^2 is thus 152 W/m^2.
Maps of surface heat flux are shown in topic 3.
3.3. Potential temperature
Pressure in the ocean increases greatly downward. A parcel of
water moving from one pressure to another will be compressed
or expanded.
When a parcel of water is compressed adiabatically, that is, without
exchange of heat, its temperature increases.
(This is true of any fluid or gas.)
When a parcel is expanded adiabatically, its temperature decreases.
The change in temperature which occurs solely due to compression or expansion is not of interest to us - it does not represent a change in heat content of the fluid. Therefore if we wish to compare the temperature of water at one pressure with water at another pressure, we should remove this effect of adiabatic compression/expansion.
Definition. "Potential temperature" is the temperature which a water parcel has when moved adiabatically to another pressure. In the ocean, we commonly use the sea surface as our "reference" pressure for potential temperature - we compare the temperatures of parcels as if they have been moved, without mixing or diffusion, to the sea surface. Since pressure is lowest at the sea surface, potential temperature (computed at surface pressure) is ALWAYS lower than the actual temperature unless the water is lying at the sea surface.
Definition. Salinity is roughly the number of grams of dissolved matter per kilogram of seawater. This was the original definition, and at one time salinity was determined by evaporating the water and weighing the residual. The dissolved matter in seawater affects its density (see section 5 below), hence the importance of measuring salinity.
The "law" of constant proportions (Dittmar, 1884), formalized the observation that the composition of the dissolved matter in seawater does not vary much from place to place. Why constant proportions? Salts come from weathering of continents and deep-sea vents, etc - the input is very very slow (order 100000 years) compared with the mixing rate of the whole ocean (which is order 1000 years). Thus it is possible to measure just one component of the dissolved material and then estimate the total amount of dissolved material (salinity). This approach was used until the 1950's.
The main constituent of sea salt is Cl, the second largest is Na, followed by many other constituents. (See Millero et al., 2008 in references below for full table.) In actuality, there is a slight variation in the proportions, and recommendations are underway to formulate new definitions of salinity which depend on the actual constituents - this may likely take the form of geographically-dependent tables of corrections to the quantity which is measured (usually conductivity).
In 2009, an international working group redefined salinity to be closer to the original definition, of the amount of dissolved matter in seawater, expressed in gm/kg. This is now called "absolute salinity". Protocols for calculating absolute salinity were developed. Papers reporting salinity are now supposed to move to using this as a standard. The standard involves two steps, one of which is approximate and likely to change over tthe years (conversion to a more correct conductivity-based reference salinity than was introduced in 1978; and inclusion of dissolved matter that does not affect the conductivity). However, the basic salinity measurement that is reported to national data archives remains the practical salinity (PSS78) (conductivity-based measurement) in order to maintain continuity of records and eliminate confusion in measuring and reporting.
Units. In the original definition, salinity units were o/oo (parts per thousand). This was replaced by the "practical salinity unit" or psu. Until recently the recommendation of the SCOR working group on salinity is that salinity be unitless, as the measurement is now based on conductivity and is not precisely related to the mass of dissolved material.
The total amount of salt in the world oceans does not change except on the longest geological time scales. However, the salinity does change, in response to freshwater inputs from rain and runoff, and freshwater removal through evaporation.
How is salinity measured? (1) Evaporate and weigh residual (oldest method). (2) Determine amount of chlorine, bromine and iodine to give "chlorinity", through titration with silver nitrate. Then relate salinity to chlorinity: S = 1.80655 C. Accuracy is 0.025 (less than 2 places). This method was used until the International Geophysical Year in 1957. (3) Measure conductivity (see next).
4.2. Conductivity
Definition.
Conductivity of sea water depends strongly on temperature, somewhat less
strongly on salinity, and very weakly on pressure.
If the temperature is measured, then conductivity can be
used to determine the salinity.
Salinity as computed through conductivity appears to
be more closely related to the actual dissolved constituents than
is chlorinity, and more independent of salt composition.
Therefore temperature must be measured at the
same time as conductivity, to remove the temperature effect and
obtain salinity. Accuracy of salinity determined from conductivity:
0.001 to 0.004. Precision: 0.001. The accuracy depends on the
accuracy of the seawater standard used to calibrate the conductivity
based measurement.
How is conductivity for calculating salinity measured? (1) For a seawater sample in the laboratory, an "autosalinometer" is used, which gives the ratio of conductivity of the seawater sample to a standard solution. The standard seawater solutions are either seawater from a particular place, or a standard KCl solution made in the laboratory. The latter provides greater accuracy and has recently become the standard. Because of the strong dependence of conductivity on temperature, the measurements must be carried out in carefully temperature-controlled conditions. (2) From an electronic instrument in the water, either inductive or capacitance cells are used, depending on the instrument manufacturer. Temperature must also be measured, from a thermistor mounted close to the conductivity sensor. Calibration procedures include matching the temperature and conductivity sensor responses.
For mapping general circulation, it is more useful to use density as our vertical coordinate than pressure since we assume that water parcels much more nearly conserve density than pressure. Thus we often map properties on isopycnal surfaces. However, the isopycnals which we choose must have the effect of changing pressure removed since most of the density variation in the ocean is due to pressure, which has no bearing on sources of heat/salt for water parcels. Thus we introduce the concept of potential density or neutral surfaces, which attempt to remove the effect of pressure changes on density.
5.1. Density
Definition. Seawater density depends on temperature, salinity and pressure. Colder water is denser. Saltier water is denser. High pressure increases density. The dependence is nonlinear. An empirical equation of state is used, based on very careful laboratory measurements. (See Gill, Appendix 3, and the fortran/matlab/c subroutines linked to the study notes.)
Units. Mass/volume.
Other expressions for density: sigma = density - 1000. alpha (specific volume) = 1/density.
Density depends nonlinearly on temperature and salinity.
The nonlinearity of the equation of state is apparent in contours
of constant density in the plane of temperature and salinity
(at constant pressure) - they are curved. They are concave towards
higher salinity and lower temperature.
5.2. Potential density
Seawater is compressible, although not as compressible as a gas.
As a water parcel
compresses, the molecules are crushed together and the density
increases. (At the same time, and for a completely different
reason, compression causes the temperature to increase which
very slightly offsets the density increase due to compression.)
Most variation in seawater is caused by pressure variation. This has little to do with the source of water, and if we wish to trace a water parcel from one place to another, one depth to another, we prefer to remove the pressure dependence. (This is in analogy with temperature; we also remove the pressure dependence in the temperature.)
We define potential density as the density a parcel has when moved adiabatically to a reference pressure. If the reference pressure is the sea surface, then we compute the potential temperature of the parcel, and evaluate the density at pressure 0 dbar. The measured salinity is used as it has very little pressure dependence.
We can also use any other pressure as a reference. We refer to potential density at the sea surface as "sigma sub theta" (Greek in class - sorry about the notes), if potential temperature is used, and "sigma sub t" if measured temperature is used. The latter is an outdated method. We refer to potential density referenced to 1000 dbar as "sigma sub 1", to 2000 dbar as "sigma sub 2", to 3000 dbar as "sigma sub 3" and so on, following the nomenclature introduced by Lynn and Reid (1973); in these cases, potential temperature relative to the reference pressure is used in evaluating the potential density.
Cold water is more compressible than warm water.
That is, it is easier to deform a cold parcel than a warm parcel.
Therefore cold water becomes denser than warm water
when they are both submerged to the same pressure.
Therefore various reference pressures are necessary. We use
a pressure which is relatively close to the depth we are
interested in studying. The compressibility effect
is apparent when we look at contours of density at say 4000 dbar
compared with those at 0 dbar.
The dependence of compressibility on temperature can be important. For instance, water spilling out of the Mediterranean through the Strait of Gibraltar is extremely salty and rather warm, compared with water spilling into the Atlantic from the Greenland Sea over the Greenland-Iceland ridge. They both have about the same density at their sills. However, the warm, saline Mediterranean water does not compress as well as the Greenland Sea water, and does not reach the ocean bottom. (There is also a difference in how the two types of water entrain other waters as they plunge downwards, so this is not a straightforward explanation.)
5.3 Neutral density
When analyzing properties in the ocean to determine where water parcels originated, it is assumed that most motion occurs with very little change in the density of the parcel, with the exception of changes due to pressure. This concept is essentially a statement that water follows an isentropic surface if it moves with no exchange of heat and salt. Defining an isentropic surface in the presence of mixing presents some difficulties. The isopycnal surfaces which we use in practice to map and trace water parcels should approximate isentropic surfaces. We typically use a reference pressure for the density which is within about 500 meters of the pressure of interest. (This pressure interval has just been found through experience to be adequate.) Therefore when working in the top 500 meters, we use a surface reference pressure. When working at 500 to 1500 meters, we use a reference pressure of 1000 dbar, etc. This discretization takes care of most of the problems associated with the effect of pressure on density. When isopycnals cover a greater range of pressure, then they must be patched into the shallower or deeper range - this is the practice followed by Reid in his various monographs on Pacific and Atlantic circulation.
Ivers (1976), working with Reid, introduced a more continuously varying reference pressure for isopycnal surfaces, which he then referred to as a "neutral surface". If a parcel is followed along its path, assuming the path is known, then it is possible to track its pressure continuously and continuously adjust its reference pressure and density.
McDougall (1987) refined the neutral surface concept and Jackett and McDougall (1997) have released a computer program and lookup table for computing neutral density. Neutral density depends on location in latitude/longitude/depth and is based on marching outwards around the world from a single point in the middle of the Pacific, using a climatological temperature/salinity data set, and tracking imaginary parcels along radiating lines.
Initial usage indicates that neutral density as determined from this program can successfully replace the approximate neutral surfaces produced by adjusting reference pressures every 1000 dbar.
Where there is a sound speed minimum, it functions as a wave guide.
The faster that sea ice is frozen, the less likely that the
salt can escape. Thus the saltiest sea ice is formed at
the lowest temperatures.
Sverdrup et al. (1942 text) tabulate the salinity
of ice formed from water which starts at salinity 30. When
frozen at an air temperature of -16C, the salinity of the
ice is 5.6. When frozen at an air temperature of -40C,
the salinity of the ice is 10.2.
Seawater properties are valuable tools for
tracing water parcels as differing water mass formation
processes imprint different amounts of various properties
on the water parcels. They are of most use when the
sources and sinks of one property
compared with another differ.
Some tracers are biogenic and hence non-conservative.
These include oxygen and the various nutrients, all discussed
very briefly
here. Some useful tracers are inert but with time-dependent
inputs, such as chlorofluorocarbons. Some useful tracers
have decay times and decay products, which can serve as a useful
measure of age. The latter are referred to as transient
tracers, and are not discussed here.
8.1. Oxygen. Non-conservative tracer. Source
is primarily air-sea interaction,
some subsurface source in outgassing by plankton. Oxygen is consumed in
situ. Oxygen content decreases with age, so it can be used in a rough way
to date the water. It is not a good age tracer because the consumption
rate is not a constant. Since waters of
different oxygen content mix, the age is not simply related to content.
Per cent saturation of oxygen depends strongly on temperature (show
figure). Cold water holds more oxygen.
Thus the per cent saturation (or related quantity "Apparent oxygen
utilization" is a better tracer than oxygen content itself.
8.2. Nitrate and phosphate: Also non-conservative. Nitrate and
phosphate are completely depleted in surface waters in the subtropical
regions where there is net downwelling from the surface and hence no
subsurface source of nutrients. In upwelling regions there is measurable
nitrate/phosphate in the surface waters due to the subsurface source
(figure from Hayward and McGowan; other figures based on woce data).
Nitrogen is present in sea water in dissolved N2 gas, nitrite, ammonia, and
nitrate, as well as in organic forms.
As water
leaves the sea surface, particularly the euphotic zone, productivity is
limited by sunlight and nutrients are "regenerated". That is, the
marine snow is decomposed by bacteria and produces nitrate and phosphate.
Nitrate and phosphate thus increase with the age of the water.
Vertical sections and maps of nitrate and
phosphate appear nearly as mirror images of oxygen, but there are important
differences in their patterns, particularly in the upper 1000 meters;
vertical extrema are not always co-located and sometime large multiple
extrema appear on one parameter and not in the others (e.g. in oxygen but
not in nitrate/phosphate).
Nitrate/oxygen and phosphate/oxygen combinations - nearly conservative
tracers. Nitrate/oxygen and phosphate/oxygen are present in seawater in
nearly constant proportions, given by the Redfield ratio. The Redfield ratio is
C:NO3:PO4:O2 = 105:15:1:135.
There are small
variations in this ratio, with particularly large deviations near the sea
surface. Because of the near constancy of this ratio, a combination of
nitrate and oxygen and of phosphate and oxygen is a nearly conservative
tracer (Broecker).
8.3 Dissolved silica - non-conservative. In seawater it is present as H2SiO4 (silicic
acid) rather than silicate (SiO3), but many people use the
term silicate.
This nutrient is also depleted in surface waters similarly to
nitrate and phosphate - completely depleted in downwelling areas and small
but measurable quantities in upwelling areas. Subsurface distributions of
silica look something like nitrate and phosphate and mirror oxygen since
silica is also regenerated in situ below the euphotic zone. However,
silica in marine organisms is associated with skeletons rather than fleshy
parts and so dissolves more slowly in the water. Much of the silica thus
falls to the bottom of the ocean and accumulates in the sediments (map of
types of sediments). Dissolution from the bottom sediments constitutes a
source of silica for the water column which is not available for nitrate,
phosphate or oxygen. Another independent source of silica are the
hydrothermal vents which spew water of extremely high temperature, silica
content, and helium content, as well as many other minerals, into the
ocean. The three named quantities are used commonly to trace hydrothermal
water.
8.4. Transient tracers.
Other tracers used commonly for ventilation and deep water circulation
include chlorofluorocarbons, tritium, helium-3 and carbon-14. CFC's and
tritium are strictly anthropogenic. Their source functions have been well
described and they are used to trace recently ventilated waters into the
ocean, and various combinations of CFC's, tritium/helium3 are used to
attach ages to water parcels, although not without approximation.
Atlases and display software
Manuals and methods:
7. Sea ice
The freezing point of seawater is lower than that of freshwater.
As sea water freezes, it forms pockets of salt. The salt
(brine) leaches out of the bottom of the ice and the brine
drips into the water below the ice. Thus sea ice when melted
is considerably fresher than the original water which was
frozen. The "brine rejection" process creates dense water
below the sea ice formation area. This can be an important
contributor to dense water formation in a global sense
as the densest waters are formed at high latitudes, and
often involve sea ice.
8. Tracers
Study questions:
Seawater properties
Subroutines for properties of seawater.
Further reading
Seawater properties (textbooks):
SIO 210 HOME
Last modified: October 3, 2019